Unique Info About How To Draw An Orthocenter

This video shows how to construct the orthocenter of a triangle by constructing altitudes of the triangle. Draw a line segment (called the altitude) at right angles to a side that goes to the opposite corner. An altitude is a line segment drawn from a vertex of the triangle perpendicular to the opposite side.

how to clean polyester fabric how to buy platinum stock how to clean a ceramic top stove how to check for a domain name how to deal with the economy crisis how to buy cheap electronics how to deal with urinary tract infection how to clean leather saddle

[solved] Task 2 A. Draw Nabc With Obtuse /c And Construct Its

Orthocenter Of A Triangle (examples, Solutions, Videos, Worksheets

How To Draw An Obtuse Triangle At

Orthocenter Of A Triangledefinitionformula Dewwool

Orthocenter Of A Triangle

Solved Construction Draw A Right Scalene Triangle And Construct Its

Steps for constructing the orthocenter of a triangle.

How to draw an orthocenter. The orthocenter is one of the triangle's points of concurrency formed by the intersection of the triangle's 3 altitudes. Connect and share knowledge within a single location that is structured and easy to search. This page shows how to construct (draw) the circumcenter of a triangle with compass and straightedge or ruler.

The orthocenter of a triangle is the point where the altitudes of the triangle intersect. Put the compasses on b and set their width to more than half the. Drawing centroid orthocentre incentre and circumcentre in a.

Label the point of intersection d. The construction starts by extending the chosen side of the triangle in both directions. These three altitudes are always concurrent.

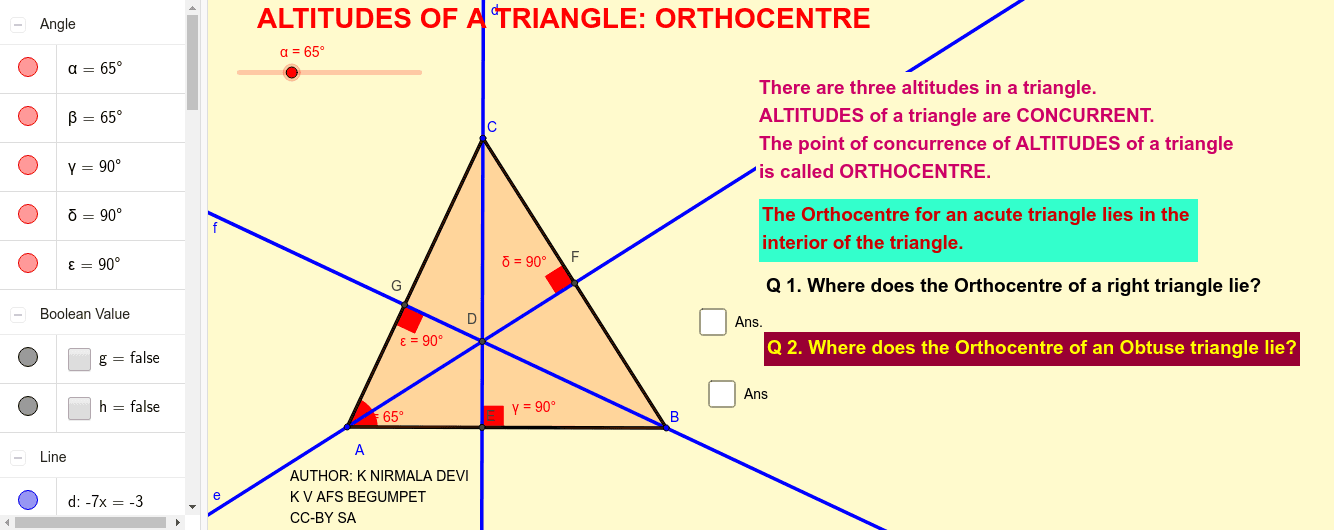
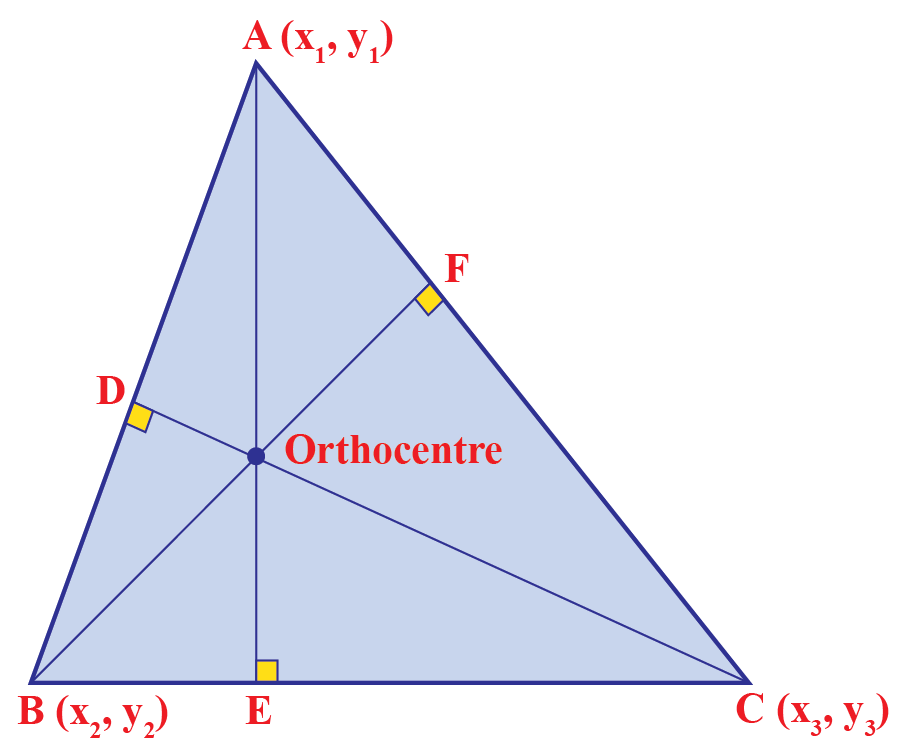
In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to (i.e., forming a right angle with) a line containing the base. Put the compasses on a and draw an arc across the side bc. The orthocenter of a triangle is the point of intersection of any two of three altitudes of a triangle (the third altitude must intersect at the same spot).

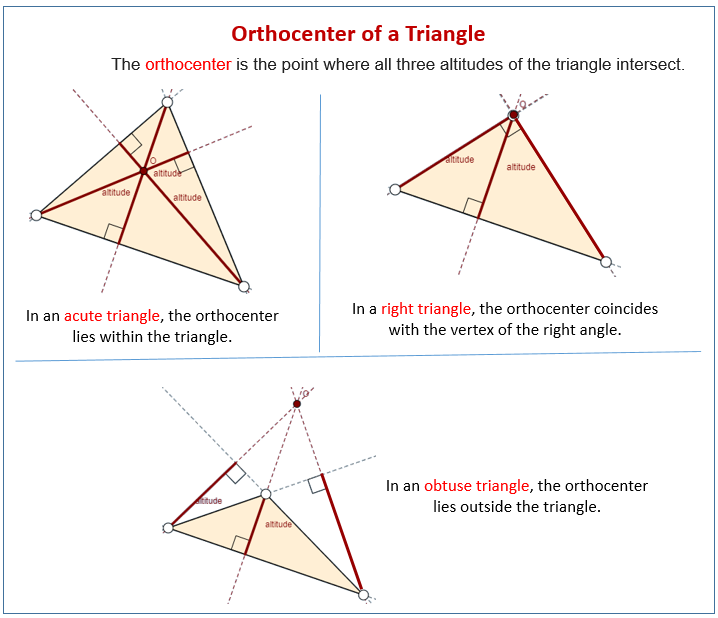
The construction uses only a compass and straight. Construct an altitude from a vertex of the triangle to the opposite side, or the line containing the opposite side. In right triangles, the orthocenter is located at the vertex opposite the hypotenuse.

This construction assumes you are already familiar with. This is done because the. 159k views 13 years ago.

See constructing the orthocenter of a triangle. In obtuse triangles, the orthocenter is located outside the triangle. Orthocenter of a triangle is a point in a triangle where all the perpendiculars drawn from the vertices to the side opposite to it, intersect each other.

The audio quality is not that great, so you'll have to. To construct the orthocenter for a triangle geometrically, we have to do the following: Find the perpendicular from any two vertices to the opposite sides.

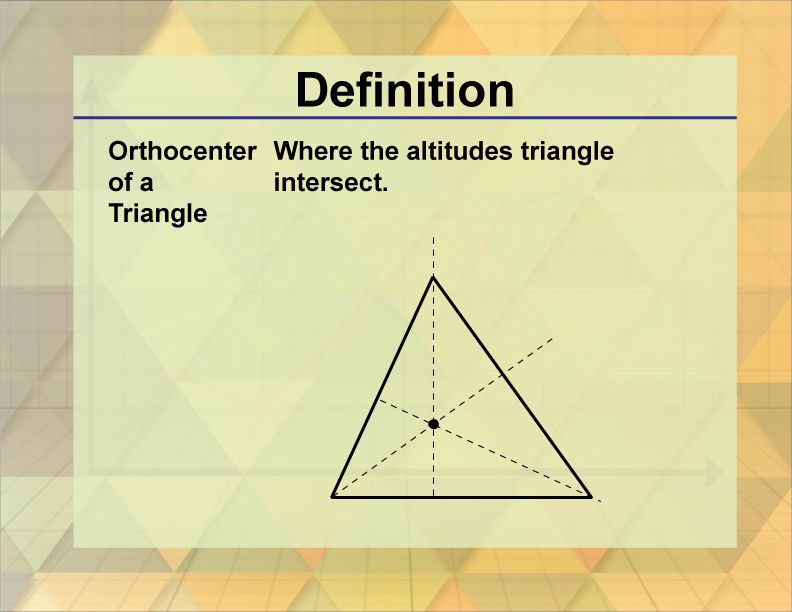
Where all three lines intersect is the orthocenter: